引言

由于大气运动的非线性混沌特征、初值误差、模式误差、有限区域模式的侧边界误差，确定性数值预报模式不可避免地存在一定的预报误差或预报不确定性(Lorenz, 1963; 杜钧和陈静, 2010; 王明欢等, 2021; 韩雨盟等, 2023; 彭飞等, 2023)，高分辨率模式的误差增长快、非线性强，其预报不确定性比低分辨率模式更大(Hohenegger and Schar, 2007; Gebhardt et al, 2011)。集合预报是解决预报不确定性的一种有效方法，可提供预报误差的概率分布(王婧卓等, 2018; Frogner et al, 2019; 潘贤等, 2021; 岳健等, 2023)。随着计算机资源的增加，2~4 km水平分辨率的区域集合预报系统应运而生，其可有效地模拟湿对流过程，进而提高对强对流天气的预报能力(Clark et al, 2018; Klasa et al, 2018; Yang et al, 2023)。高分辨率区域集合预报模式已成功应用到德国、英国、美国、法国等全球多个业务数值天气预报中心(Golding et al, 2014; Gallo et al, 2017; Hagelin et al, 2017; Schellander-Gorgas et al, 2017)。

高分辨率区域集合预报的关键是如何采用合理的扰动方法来描述数值预报模式的多源误差(Vié et al, 2011; Raynaud and Bouttier, 2016)。目前，已有大量学者针对高分辨率区域集合预报的初值扰动和模式扰动方法开展了相关研究(Lawson and Gallus, 2016; Wastl et al, 2019; Zhang, 2019; Ono et al, 2021; Xu et al, 2022; 张涵斌等, 2022; Wang et al, 2023a; 2024)，从预报时效、天气类型、变量、扰动尺度等多个角度分析了初值扰动和模式扰动对高分辨率区域集合预报的影响，且有针对性地构建了适用于该系统的初值和模式扰动方法，揭示了两者的相互作用机制等。除初值扰动和模式扰动外，受限于有限区域，侧边界扰动也是高分辨率区域集合预报的一种主要扰动方法(Peralta et al, 2012)。2~4 km水平分辨率的集合预报模式由于更高的分辨率和更小的预报范围，其对侧边界扰动的敏感性要高于中尺度集合预报模式(庄潇然等, 2017)。侧边界扰动方法主要包括两类: 第一类方法是采用全球或区域集合预报动力降尺度产生侧边界扰动(Storto and Randriamampianina, 2010; 张涵斌等, 2017; 庄潇然等, 2017)，以获得大尺度不确定性信息，该类方法是各大数值预报中心的主流方法(Vié et al, 2011; Caron, 2013); 第二类是尺度化滞后平均法(Hou et al, 2001; Kong et al, 2007)。范宇恩等(2019)对比了两类侧边界扰动方法，结果表明，动力降尺度侧边界扰动方法的等压面要素和地面要素的集合预报技巧要明显优于尺度化滞后平均法，即动力降尺度构造的侧边界扰动更加合理。

侧边界扰动对区域集合预报的影响研究已有很多。大量研究(Hou et al, 2001; Nutter et al, 2004a; 2004b)表明，如果没有引入侧边界扰动，区域模式的离散度会较低，而引入侧边界扰动可提高集合预报的离散度，同时，侧边界扰动可降低集合平均均方根误差(Saito et al, 2010)。侧边界扰动对集合预报的影响不仅与预报时效有关(Gebhardt et al, 2011; Vié et al, 2011; Marsigli et al, 2014)，也与误差传播速度和区域大小有关(Peralta et al, 2012)，具体而言，侧边界扰动的影响随着预报时效的延长而逐渐增加，随着区域的减小而增加。另外，侧边界扰动对集合预报的影响具有环流依赖性，即侧边界扰动对强强迫个例的影响大于对弱强迫个例的影响(Zhang et al, 2023)。

中国气象局区域集合预报系统(CMA-REPS)是由地球系统数值预报中心自主研发的，其确定性模式为中国气象局中尺度模式(CMA-MESO模式)(王婧卓等, 2021)。鉴于侧边界扰动对高分辨率区域集合预报的影响，如何构建适用于CMA-REPS的侧边界扰动方法，描述CMA-MESO模式的侧边界不确定性，并实现较好的离散度技巧关系是本文的研究重点。鉴于此，利用中国气象局全球集合预报系统(CMA-GEPS)扰动场信息及确定性模式CMA-MESO的侧边界场，构建了混合侧边界扰动方法，并采用动态扰动系数调整方案对侧边界扰动大小进行约束，以期获得较好的集合预报离散度技巧关系。开展本研究有利于加深对侧边界扰动对高分辨率区域集合预报影响的认识，构建合理且业务可行的侧边界扰动方法，进而提高集合预报的离散度技巧关系和概率预报技巧。

1 模式和方法 1.1 CMA-REPS V4.0简介

CMA-MESO确定性模式具有全可压非静力平衡的动力框架、半隐式半拉格朗日时间平流方案、水平Arakawa-C网格、垂直地形追随坐标(于翡等, 2018)。基于CMA-MESO V5.1版本，中国气象局地球系统数值预报中心发展了3 km水平分辨率的中国气象局区域集合预报系统CMA-REPS V4.0版本，并已于2024年11月实现业务化升级。CMA-REPS V4.0参数配置见表 1：垂直层次51层，预报时效72 h(均为世界时)，模拟范围覆盖中国区域(10°~60.1°N、70°~145°E)；控制预报初值和侧边界来源于0.5°×0.5°分辨率的美国国家环境预报中心全球预报系统(NCEP-GFS)(于翡等, 2018; 陈静等, 2022)；集合成员同化分析系统采用常规观测资料扰动、三维变分(3DVAR)资料同化、云分析方案(朱立娟等, 2017)；初值扰动采用多尺度奇异向量最优谱截断混合初值扰动(叶璐等, 2020; Liu et al, 2024)与观测资料扰动(张涵斌等, 2022)组合；模式扰动采用随机物理倾向扰动方案(袁月等, 2016; Xu et al, 2022)；侧边界扰动采用混合侧边界扰动方法；集合成员数为15个，包括1个控制预报和14个扰动成员。

1.2 混合侧边界扰动方法

CMA-REPS V4.0控制预报侧边界来源为NCEP-GFS。同时，为表征0.5°×0.5°分辨率的CMA-GEPS的预报不确定性，构建了混合侧边界扰动方法。即提取CMA-GEPS扰动成员相对于控制预报的全球背景预报扰动场，乘以侧边界扰动系数，并加在控制预报全球背景驱动数据上构造全球混合背景场，并通过动力降尺度得到各成员的侧边界集合，具体如式(1)和式(2)所示。侧边界扰动变量为纬向风u和经向风v。

$ \begin{array}{ll} \mathrm{BP}_i=\mathrm{BG}_i-\mathrm{BG}_0 & i=1, 2, 3, \cdots, 14\end{array} $

(1)

$ \begin{array}{ll} \mathrm{BM}_i=\mathrm{BC}_0+\mathrm{BP}_i \times r(k) & i=1, 2, 3, \cdots, 14 \end{array} $

(2)

式中：i代表第1~14个扰动成员，BG_i为扰动成员i的全球背景场，BG₀为CMA-GEPS控制预报的全球背景场，BP_i为CMA-GEPS全球背景预报扰动场，r(k)为第k层等压面的侧边界扰动系数，BC₀为CMA-REPS V4.0控制预报的背景场(来自于NCEP-GFS)，BM_i为CMA-REPS V4.0所需的全球混合背景场。

基于上述方案，进一步根据CMA-REPS V4.0的历史集合平均均方根误差(RMSE)和集合离散度关系构建了一套动态混合侧边界扰动方案，以实现高分辨率区域集合预报集合离散度与均方根误差之间较好的一致性。该方案是在模式积分后运行。需要指明的是，计算集合平均均方根误差时，以控制预报的分析场作为真值，考虑到业务时效性问题，对于某一起报时次，只能获得起报时次前3 d(72 h，对应模式预报时效)预报的均方根误差。动态混合侧边界扰动方案计算流程如下：(1)计算起报时次前3~13 d(每日两个时次，00时和12时)不同垂直层次、不同预报时效(不包括初始时刻，因为初始时刻扰动大小主要是由初值扰动所影响)的纬向风u、经向风v的集合平均均方根误差和集合离散度；(2)计算集合平均均方根误差和集合离散度的比值，并将比值进行预报时效、起报时次、2个变量的平均，得到不同垂直层次的侧边界扰动系数r(k)，用于下一时次起报的混合侧边界扰动方案构建[式(1)和式(2)]。第k层的r(k)计算公式如式(3)所示：

$ \begin{gathered} r(k)=\frac{1}{2} \times \frac{1}{20} \sum\limits_{j=1}^{20} \frac{1}{t} \times \\ \sum\limits_{n=1}^t\left[\frac{\operatorname{RMSE}_u(k, j, n)}{\operatorname{spread}_u(k, j, n)}+\frac{\operatorname{RMSE}_v(k, j, n)}{\operatorname{spread}_v(k, j, n)}\right] \end{gathered} $

(3)

式中：RMSE_u(k, j, n)和RMSEv(k, j, n)、spreadu(k, j, n)和spreadv(k, j, n)分别为第k层等压面第n个预报时效、第j个起报时次的CMA-REPS V4.0模式的纬向风u和经向风v的集合平均均方根误差、集合离散度。k取值范围在1~26, 对应1000~10 hPa；n取值范围在1~6, 即t=6；j取值范围在1~20，即10 d共20个时次。

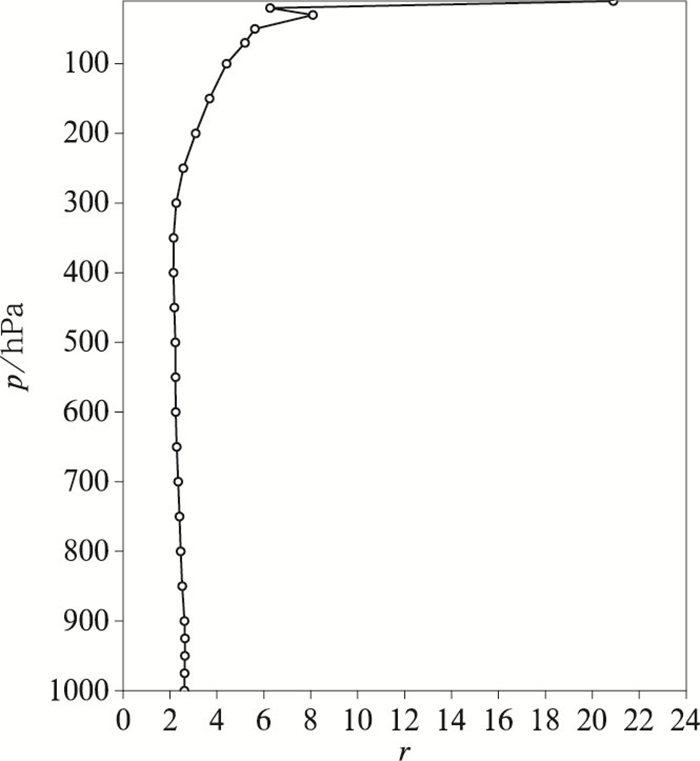
图 1给出了不同垂直层次的侧边界扰动系数分布。根据其定义可知，理想情况下，r(k)的值应为1，即集合离散度与集合平均均方根误差相等。然而，从图 1中可以看出，r(k)在所有垂直层次上均大于1，说明集合平均均方根误差远大于集合离散度，这在国际上大多数集合预报系统中是较为普遍的现象(McCollor and Stull, 2009; Garcia-Moya et al, 2011)。另外，高层变量的离散度技巧关系更差，这可能与扰动方案对高层变量不确定性的捕捉能力不足，或者高层变量存在较大的系统性误差有关(Wang et al, 2018)，未来需进一步研究。

1.3 试验设计和检验指标

为揭示侧边界扰动对高分辨率区域集合预报的影响，并构造合理的集合预报侧边界扰动方案，共设计了3组试验，具体试验名称及设计方案见表 2。相互间进行对比，目的一在于揭示混合侧边界扰动方案相比于无侧边界扰动方案的作用，目的二在于阐述动态混合侧边界扰动方案相比于混合侧边界扰动方案的优势。需要说明的是，为单独说明侧边界扰动的作用，不同试验均采用相同的初值扰动和模式扰动方案。

本文对扰动能量演变特征、等压面要素和降水的离散度技巧关系、概率预报技巧进行了检验。差异总能量(DTE)、整层扰动能量(RMDTE)、扰动谱分布(Nielsen and Schumacher, 2016; 马雅楠等, 2023)用来表征扰动能量的演变特征；RMSE、集合离散度、集合一致性(RMSE与集合离散度的比值，一致性越接近于1，集合预报离散度技巧关系越好)(Du et al, 2014)、连续分级概率评分(CRPS)(Bröker, 2012)用来检验等压面要素的集合预报技巧；误差分数技巧评分(eFSS)和离散分数技巧评分(dFSS)(Dey et al, 2014)用来评估降水的离散度技巧关系，邻域降水概率预报技巧评分(Brier)(Wang et al, 2022)用来评估降水的概率预报技巧。具体的检验指标公式可参考以往研究(Wang et al, 2022；2023a；2023b)。

采用CMA-MESO模式的分析场作为等压面要素检验的真值；采用5 km×5 km水平分辨率的地面-卫星-雷达三源融合降水格点数据作为降水检验的真值，并通过双线性插值方法将其转换到3 km×3 km水平分辨率的模式网格中(潘旸等, 2015)。

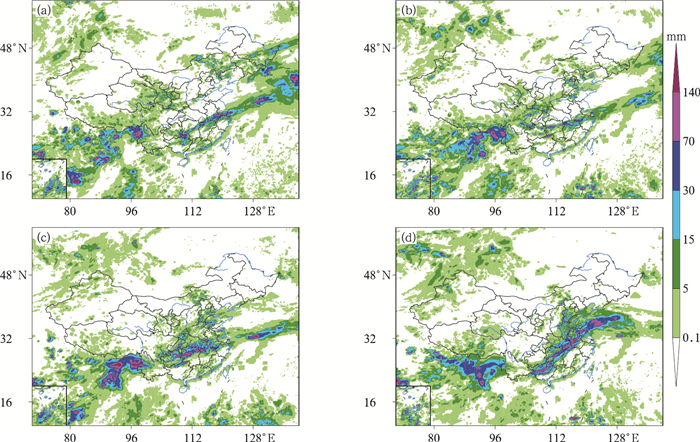
本文对2024年6月30日00时、12时及7月1日00时、12时进行了连续4个时次的预报。受高空槽、低空急流等共同影响(霍达等, 2024)，此时段出现了强降水过程(图 2)，主雨带呈东北—西南走向，安徽、湖北、湖南、江西、贵州、广西等地均出现强降水。文中检验结果均为4个时次预报统计平均的结果。

本文所有附图涉及的地图均基于国家测绘地理信息局标准地图服务网下载的审图号为GS(2019)1786号的标准地图制作，底图无修改。中国全图比例尺为1∶20 000 000，南海诸岛地图比例尺为1∶40 000 000。

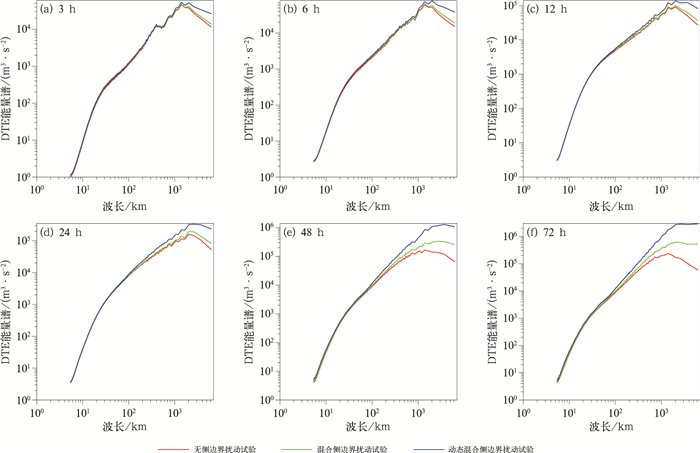
2 扰动能量演变特征 2.1 扰动能量谱特征

图 3给出了不同预报时效集合平均的500 hPa的DTE能量谱分布。能量谱分布可给出扰动的尺度分布特征。试验对比表明，无侧边界扰动试验的扰动总能量谱最小，加入侧边界扰动有利于提高扰动总能量谱，尤以预报中后期的扰动能量谱提高最为显著，说明侧边界扰动对高分辨率区域集合预报的影响随着预报时效的延长而逐渐增加，与前人的研究结果相吻合。另外，混合侧边界扰动试验可明显提高无侧边界扰动试验在波长100 km以上的DTE能量谱，这与混合侧边界扰动试验相比于无侧边界扰动试验的DTE能量谱增长率在不同波长分布是吻合的(图略)，说明侧边界扰动有利于提高α中尺度和大尺度波长范围内的扰动能量。侧边界扰动主要对较大尺度波长范围的扰动能量有影响，这是因为该扰动来自于全球集合预报动力降尺度形成，只能分辨相对大尺度的扰动信息，与以往研究(庄潇然等, 2017; 范宇恩等, 2019; Zhang et al, 2023)结论是一致的。而动态混合侧边界扰动试验可进一步提高混合侧边界扰动试验在波长100 km以上的波谱能量，即在保持小尺度扰动能量基本不变的情况下，进一步增加了大尺度扰动能量。其他垂直层次的DTE能量谱分布类似，不再赘述。

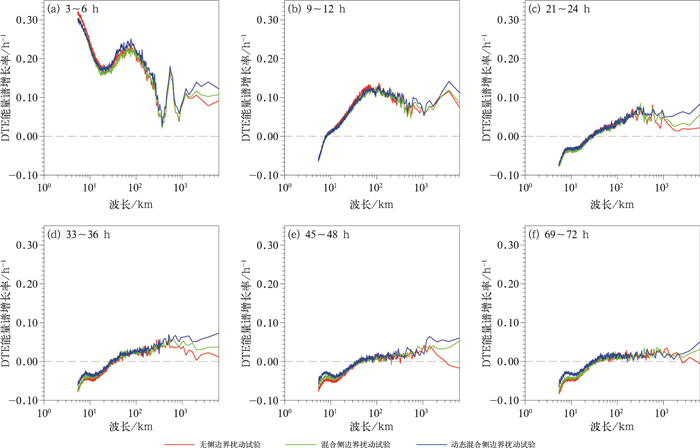
为了表征扰动能量的增长特征，采用Lyapunov指数增长率(Kay and Kim, 2014; Wang et al, 2021)计算DTE能量谱随预报时效的增长率。由图 4可见，对3组侧边界扰动试验而言，在前6 h小尺度扰动快速增长，随着预报时效增加，扰动增长率逐渐降低，甚至在波长50 km以下范围内为负值，即小尺度扰动在预报初期快速增长，随后达到饱和。对100 km以上的α中尺度和大尺度波长而言，无侧边界扰动试验在预报初期的DTE能量谱增长率较大，随着预报时效增加，增长率逐渐降低并趋近于零。这说明无侧边界扰动的能量谱在预报初期(前36 h)随预报时效增加而逐渐增长，即扰动逐渐发展，但是在预报后期，扰动能量谱增长缓慢，即高分辨率区域集合预报没有加入侧边界扰动会抑制预报后期扰动能量的增长。然而，两组侧边界扰动试验的扰动能量谱增长率均为正值，且大于无侧边界扰动试验的能量谱增长率，说明侧边界扰动可促进扰动能量的增长，且动态混合侧边界扰动方案相比于混合侧边界扰动方案在大尺度波长内的能量谱增长率更快，即扰动发展更快。

2.2 扰动能量特征

为表征扰动能量的分布特征，图 5给出了不同预报时效500 hPa的DTE分布。从图中可见，3组方案的扰动总能量随着预报时效增加均呈增长趋势，即扰动能量逐渐发展，且扰动总能量水平分布大值区基本相当，如在12 h预报时效，扰动总能量大值区均分布在侧边界及中国东北和华北地区。试验对比结果表明，在3 h预报时效下，混合侧边界扰动试验相比于无侧边界扰动试验的扰动总能量有所增加，且增量主要集中在模拟区域的边界处，即侧边界扰动在预报初期主要作用在模式的侧边界处，随着预报时效的延长，侧边界扰动向中心区域扩展，带来整个区域的扰动能量增量。而动态混合侧边界扰动试验的扰动总能量要大于混合侧边界扰动试验，尤以预报中后期扰动能量增加最为显著。扰动能量的垂直分布特征与水平分布特征一致，不再赘述。

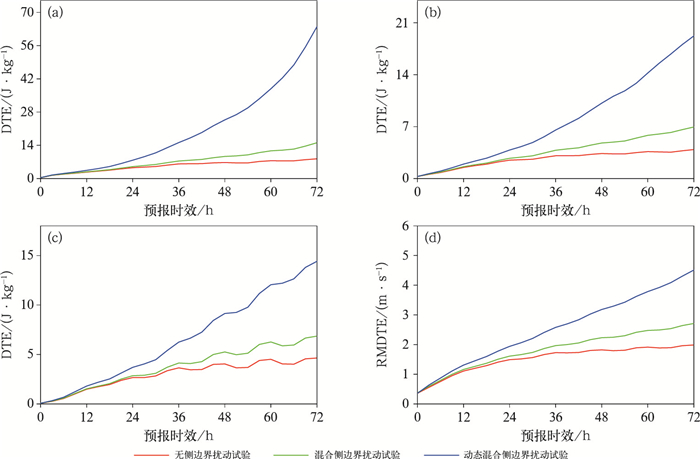
为表征扰动能量随预报时效的演变特征，图 6给出了不同垂直层次的DTE和整层RMDTE随预报时效的演变。从图中可见，无侧边界扰动试验在前36 h的扰动能量增加速度较快，在36 h以后扰动能量增加速度缓慢。相比于无侧边界扰动试验，混合侧边界扰动试验可明显增加扰动能量，且侧边界扰动的影响随着预报时效延长而更加明显。动态混合侧边界扰动试验可进一步增加扰动能量，使得扰动增长率更快。提高的扰动增长率有望进一步改进目前国际集合预报系统普遍存在的集合离散度不足的问题，提高集合预报技巧。

3 等压面要素集合预报技巧 3.1 离散度技巧关系

图 7给出了不同预报试验500 hPa纬向风的集合平均均方根误差、集合离散度、集合一致性在72 h预报时效的水平分布。从图中可见，3组试验的均方根误差水平分布基本相当，大值区均分布在中国东北地区。然而，3组试验的集合离散度差异较为明显，具体表现为：无侧边界扰动试验的集合离散度最小，最大值在4.2~4.9 m·s^-1；混合侧边界扰动试验的离散度明显增加，尤以侧边界处离散度增加最为明显；动态混合侧边界扰动试验相比于混合侧边界扰动试验的离散度有所增加，这与扰动能量的演变特征是一致的。为了更直观地反映集合平均均方根误差和集合离散度的关系，图 7也给出了集合预报一致性的水平分布。从图中可见，无侧边界扰动试验的集合预报一致性在中国大部分区域均大于1，说明试验均存在集合离散度不足的问题；混合侧边界扰动试验的集合预报一致性明显降低，某些区域的集合一致性大于1，某些区域的集合一致性小于1，整体围绕在1附近，集合离散度技巧关系更好；动态混合侧边界扰动试验的集合离散度进一步增大，使得集合预报一致性更低，但该试验是否相比于混合侧边界扰动试验更好，需结合RMSE、离散度的区域平均值和两者的比值来说明。

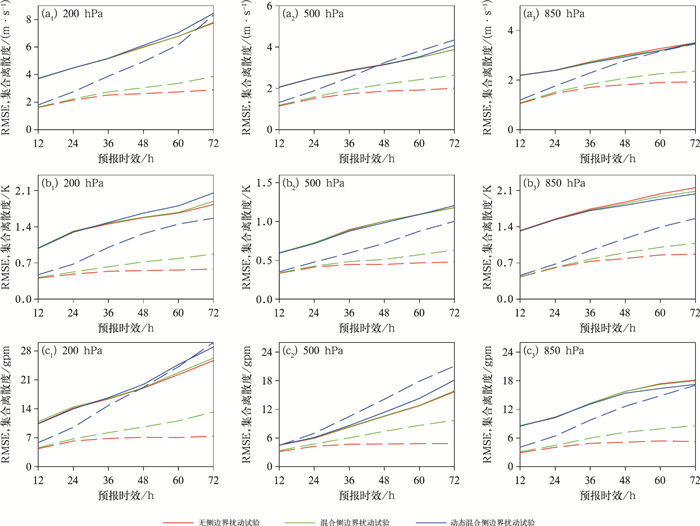
图 8给出了200、500、850 hPa的纬向风、温度、位势高度区域平均的集合平均均方根误差、集合离散度随预报时效的演变。从图中可见，对无侧边界扰动试验而言，集合离散度远小于集合平均均方根误差，说明无侧边界扰动存在集合离散度不足的问题。另外，相比于无侧边界扰动试验，两组混合侧边界扰动试验可降低850 hPa的纬向风、温度、位势高度的集合平均均方根误差，但却增加了200 hPa和500 hPa不同变量的均方根误差，说明侧边界扰动可改进低层集合平均均方根误差，但对中高层则有一定的负效果。集合离散度的对比结果表明，无侧边界扰动试验的集合离散度最小，混合侧边界扰动试验的集合离散度有一定的提升，离散度技巧关系更好，动态混合侧边界扰动试验可进一步增加集合离散度，对除500 hPa位势高度外的大部分变量和垂直层次而言，离散度技巧关系更好。

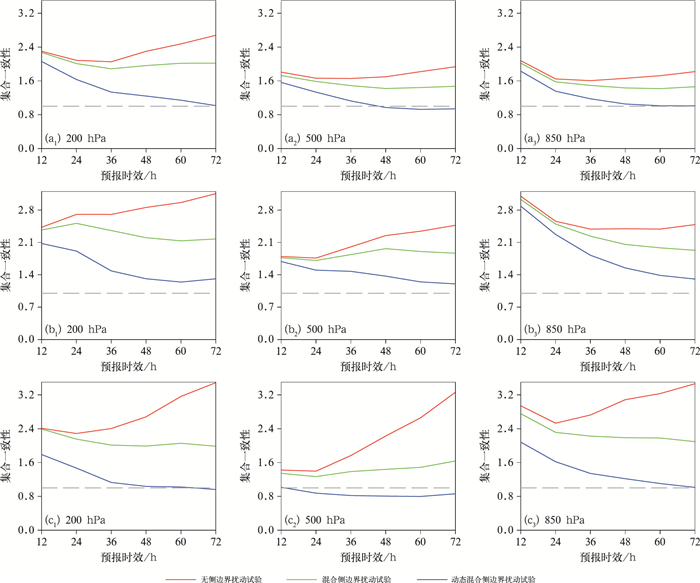
图 9给出了200、500、850 hPa的纬向风、温度、位势高度的集合一致性随预报时效的演变。集合一致性是用区域平均的集合平均均方根误差与区域平均的集合离散度求比值计算得到，即图 8中实线与虚线的比值。从图中可见，对无侧边界扰动试验而言，不同层次不同变量的集合一致性远大于1，与图 8的结论是一致的，且位势高度和高层的纬向风、温度的一致性更大，即这些变量存在明显的集合离散度不足的问题。相比于无侧边界扰动试验，混合侧边界扰动试验的集合预报一致性更接近于1，离散度技巧关系有所改进，且预报中后期改进更为明显，这说明该试验的离散度增长率要高于均方根误差增长率。另外，除500 hPa位势高度外，动态混合侧边界扰动试验可明显改进混合侧边界扰动试验集合离散度不足的问题，离散度技巧关系更好。集合一致性垂直分布也有相同的结果，不再赘述。需要说明的是，动态混合侧边界扰动试验的500 hPa位势高度集合一致性小于1，表明出现了超离散现象。这可能是因为该试验使得500 hPa纬向风的集合离散度增加，由风场约束的位势高度成员差异也会进一步增大，最终，这种过大的离散度超过了集合平均均方根误差的量级。综合而言，动态混合侧边界扰动方案在保证各变量之间动力协调的同时，提高了大部分垂直层次和变量的离散度技巧关系。

另外，近地面要素的离散度技巧关系(图略)与低层等压面要素一致，即相比于无侧边界扰动试验，混合侧边界扰动试验的集合一致性更接近于1。相比于混合侧边界扰动试验，动态混合侧边界扰动试验可进一步改进离散度技巧关系，尤以预报后期的改进最为明显。

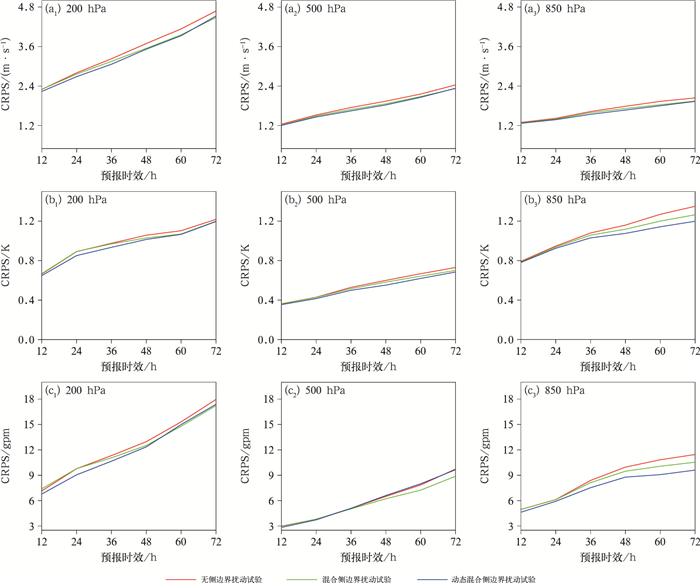
3.2 概率预报技巧

图 10给出了不同垂直层次不同变量的概率预报技巧评分随预报时效的演变。从图中可见，对大部分变量而言，无侧边界扰动试验的CRPS最高，集合预报概率预报技巧最差。混合侧边界扰动试验的CRPS有所降低，概率预报技巧更好。对850 hPa位势高度和温度而言，动态混合侧边界扰动试验的CRPS要低于混合侧边界扰动试验，尤以预报后期的改进最为明显。综合而言，侧边界扰动可明显改进等压面要素的概率预报技巧，动态混合侧边界扰动试验可进一步改进混合侧边界扰动试验的低层等压面要素的概率预报技巧。

4 降水集合预报技巧 4.1 离散度技巧关系

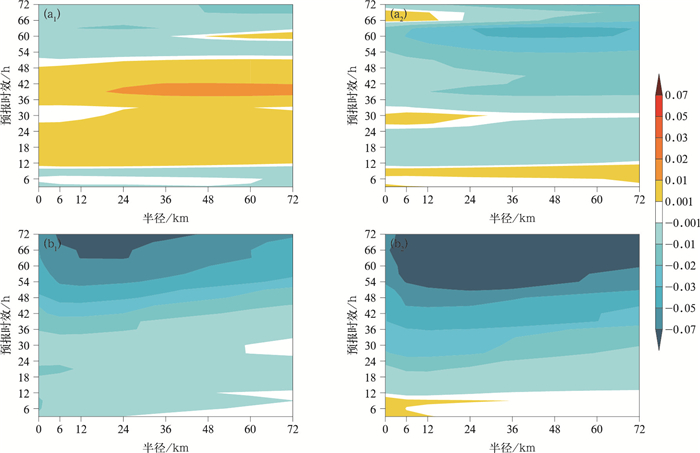
图 11给出了3 mm·3 h^-1降水阈值下不同试验的eFSS和dFSS差异。eFSS越低，代表降水预报误差越大，dFSS越低，代表降水离散度越大。试验对比说明，相比于无侧边界扰动试验，混合侧边界扰动试验的eFSS在不同预报时效表现存在差异：在12~54 h预报时效的降水预报误差降低，在前12 h和后18 h的降水预报误差则略有增加。dFSS的情况，混合侧边界扰动试验明显小于无侧边界扰动试验，尤其以预报后期的差异更为明显，说明混合侧边界扰动试验可提高无侧边界扰动试验的降水离散度，且侧边界扰动对降水离散度的影响随预报时效增长更加明显，这与等压面要素的表现一致。因为降水离散度小于降水预报误差(图略)，混合侧边界扰动方案在12~54 h预报时效内更高的降水离散度和更低的降水预报误差带来更好的降水离散度技巧关系。另外，由于dFSS差异在前12 h和后18 h预报时效内大于eFSS差异，故更大的降水离散度带来更好的降水离散度技巧关系。同理，相比于混合侧边界扰动试验，动态混合侧边界扰动试验可增加大部分预报时效的降水预报误差和降水离散度。由于降水预报误差的差异小于降水离散度的差异，故动态混合侧边界扰动试验可进一步提高降水的离散度技巧关系。其他降水阈值表现一致，在这里不再赘述。

4.2 概率预报技巧

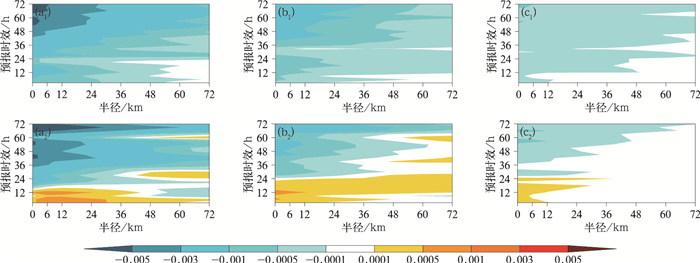
图 12给出了不同试验的降水邻域概率技巧评分差异。Brier越小，降水的概率预报技巧越高。从图中可见，无论对任何降水阈值而言，混合侧边界扰动试验的Brier均小于无侧边界扰动试验，说明侧边界扰动可提高降水的概率预报技巧，尤以预报后期的改进最为明显。另外，对24 h以后的大部分预报时效而言，动态混合侧边界扰动试验的Brier均低于混合侧边界扰动试验，说明动态扰动试验的中后期降水概率预报技巧更好；在0~24 h预报时效内，则高于后者，这是因为在没有观测到降水的区域，动态混合侧边界扰动试验的降水邻域集合概率高于无侧边界扰动试验的降水概率(图略)。这表明邻域集合概率与观测降水之间的关系能够很好地解释三种侧边界扰动方案在降水概率预报技巧上的差异，与Wang et al(2024)的研究结果一致。

5 结论和讨论

本文充分利用我国自主研发的CMA-GEPS扰动场信息及确定性模式CMA-MESO的侧边界场，构建了混合侧边界扰动方法，并采用动态扰动系数调整方案对侧边界扰动大小进行约束，以期获得较好的集合预报离散度技巧关系。开展本研究有利于揭示侧边界扰动对高分辨率区域集合预报的影响，并构建业务可行的CMA-REPS V4.0侧边界扰动方法及业务系统，进而提高集合预报等压面要素和降水的预报技巧。研究结论如下：

(1) 能量谱分布表明，无侧边界扰动会抑制预报后期能量谱增长，混合侧边界扰动试验有利于提高α中尺度和大尺度波长范围内的扰动能量谱，且对预报中后期影响更为显著，动态混合侧边界扰动试验在保持小尺度波谱能量不变的情况下，可进一步提高混合侧边界扰动试验在波长100 km以上的波谱能量。

(2) 能量演变特征表明，无侧边界扰动试验在36 h扰动能量基本达到饱和，后期扰动能量增长缓慢；混合侧边界扰动试验可提高扰动能量，且在初期主要作用在侧边界处，随着预报时效的增加，侧边界扰动向中心区域扩展，带来整个区域的扰动能量增量；动态混合侧边界扰动试验可进一步提高混合侧边界扰动试验的扰动能量，使得扰动增长率更快。

(3) 相比于无侧边界扰动试验，混合侧边界扰动试验可提高等压面要素和降水的离散度技巧关系和概率预报技巧；动态混合侧边界扰动试验可进一步增加混合侧边界扰动试验的集合离散度，降水和等压面变量的集合一致性更接近于1，且可提高低层等压面要素和24 h预报时效以后的降水概率预报技巧。

综合而言，通过高分辨率区域集合预报模式历史的均方根误差和离散度关系构建的动态混合侧边界扰动方案对等压面要素和降水均有较好的集合预报技巧，已应用到业务CMA-REPS V4.0中。需要说明的是，首先，初值扰动和模式扰动对高分辨率区域集合预报的影响依然很大，需进一步开展相关研究。在此基础上，根据CMA-REPS V4.0的历史均方根误差和离散度关系，对侧边界扰动系数进行调整，以构建更为合理的侧边界扰动方案。其次，本文是通过与全球集合预报相耦合来获得高分辨率区域集合预报的侧边界扰动场，这也是很多业务和科研机构采用的主流方法(Wang et al, 2011; Zhang et al, 2015)。然而，通过全球集合预报系统动力降尺度获得的侧边界扰动可能存在预报误差(Marsigli et al, 2014)，需采用一个中间分辨率的区域集合预报为2~4 km水平分辨率的高分辨率集合预报系统提供侧边界条件扰动(Caron, 2013; 庄潇然等, 2017)。因此，未来可就此开展研究，并分析其集合预报效果。最后，本文所有结果均为4个预报时次的平均值。随着计算机资源的不断增加，未来需开展更多的批量试验，以更全面地揭示所构建的动态混合侧边界扰动方案的效果，并分析其与其他试验的统计学差异。